Archive for 2009
El campesino, el lobo, la oveja y la col
Cruzar un río no supone un problema si se dispone, por ejemplo, de un puente. Pero en determinadas circunstancias.
Etiquetas :
Matemática recreativa,
Recursos para docentes,
Operaciones Combinadas
El Portal genmagic.org. es un espacio que responde a la necesidad de facilitar a los profesionales de.
Torres de Hanoi
Las Torres de Hanói es un juego matemático inventado en 1883 por el matemático francés Éduard Lucas..
Resta sin Parar
Esta aplicación permite realizar restas sencillas con números dispuestos en un cuadrado debiendo obtener.
¿Cómo enseñar para que los alumnos aprendan?
La respuesta a esta cuestión es lo que se pretende analizar el libro "Aprender a enseñar" de Oriol Amat..
Etiquetas :
Libros,
Recursos para docentes,
Math puzzles and brainteasers: grades 6-8
Una gran colección de enigmas de matemática para los estudiantes en grados 6-8. Incluye más de 300 actividades.
Reflexiones Didacticas: en torno a fracciones, razones y proporciones
Este modulo presenta una mirada a las distintas facetas de las fracciones, desde una perspectiva didáctica,.
COLECCIÓN MINERVA: Ecuaciones Diferenciales Ordinarias
Ecuaciones Diferenciales Ordinarias es un texto que conduce al lector, en forma eficaz, a la comprensión.
Etiquetas :
Educación Superior,
Libros,
100 formas de animar grupos
100 Formas de Animar Grupos: Juegos para usar en Talleres, Reuniones y la Comunidades, es una serie.
Traductor portable: Globalink Power Translator
Hoy en día todo el mundo necesita disponer de un buen traductor, y si encima se trata de un traductor.
Etiquetas :
Software,
E-Z Geometry: Lawrence S. Leff
Conocido por muchos; esta nueva edicion ofrece un tratamiento moderno. Los libros de E-Z son manuales.
Psicología Educativa: Anita Woolfolk
Muchas de las personas que leerán este libro quizás estén inscritas en un curso de psicología educativa,.
La Geometría en el Entorno
Aquí les dejo un vídeo sobre la Geometría, en este se muestran esculturas, monumentos, edificios, etc..
Geometria: Teorema de Thales
En muchos videos que encuentras por Internet puedes ver como resolver problemas de la vida cotidiana.
La fotografía más famosa de la historia de la Ciencia: La Conferencia Solvay
A lo largo de la historia de la Ciencia ha habido muchas reuniones de científicos de todas las ramas.
Etiquetas :
Curiosidades,
La habitación de Fermat (2007)
Cuatro matemáticos son citados a una reunión secreta en la que tendrán que poner a prueba su ingenio.
Etiquetas :
Cine,
Algebra con papas
Algebra con papas es un conjunto de actividades interactivas de Álgebra para Educación Secundaria..
142857
Este número, el 142857, es de los denominados cíclicos, ya que tiene la particularidad que al ser multiplicado.
Etiquetas :
Curiosidades,
Chat Noir: juego en flash
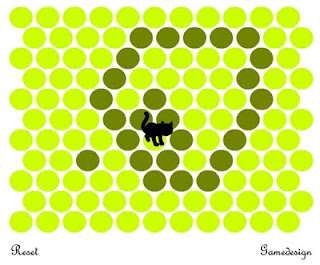
Chat Noir es un juego en flash en el que deberás evitar que el gato escape del tablero. Para ello deberás.
Etiquetas :
Juegos,
Nunca dividas por cero
La división por cero en matemáticas es una operación no definida en los números naturales, enteros y.
Etiquetas :
Videos,
Puzzle con números romanos
Unos sencillos puzzles matemáticos con números romanos. Basta con añadir una sola linea en cada ecuación.
Etiquetas :
Juegos,
1, 11, 21, 1211, 111221, 312211, ...
Los problemas de secuencias numéricas son clásicos en las matemáticas recreativas. La secuencia de números.
Etiquetas :
Curiosidades,
La Balanza
¿Sabes utilizar una balanza? Si no sabes usarla no te preocupes, con esta sencilla animación puedes.
Geo Plano
Con Geoplano aprenderás de manera divertida a calcular perímetros y áreas de figuras entre otras ac.
Reloj infinito
Preciosa imagen al más puro estilo escheriano que extiende el reloj en una espiral hasta el infinito..
Etiquetas :
Curiosidades,
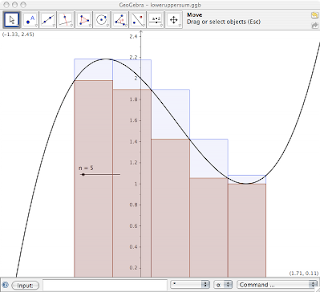
Enciclopedia Interactiva de Matemática
Este es un consultor multimedia de matemática en dónde el entretenimiento y aprendizaje de esta asignatura.
Etiquetas :
Educación Secundaria,
Recursos para docentes,
Demostraciones Geométricas
Sumas de Potencias- La suma de las fracciones que tienen como denominador potencias de 2 es 1.1/2 +.
Etiquetas :
Aritmética,
Recursos para docentes,
Números, Grupos y Anillos
El libro es una introducción a los temas clásicos de álgebra abstracta y moderna con problemas por resolver..
Etiquetas :
Educación Superior,
Libros,
Aproximaciones del número π
Navegando por la red encontré algunas páginas dedicadas a aproximar el número π. Allí aparecen algunas.
Etiquetas :
Curiosidades,
Problemas y Ejercicios de Análisis Matemático
El libro “problemas y ejercicios de análisis matemático” se destina a los alumnos de ciencias que estudian.
Etiquetas :
Educación Superior,
Libros,
El taller: una alternativa de renovación pedagógica
Hablar de "crisis en la educación" se ha convertido en algo común... Tan común como hablar de experiencias.
NUMBER THEORY: an introduction mathematics
Estos 2 volúmenes son una introducción moderna a la Teoría de Números, enfatizando sus conexiones con.
Etiquetas :
Aritmética,
Libros,
Geometria: Marcel Berger
Marcel Berger presenta 2 volúmenes de Geometría, que sirven como una fuente de referencia comprensible.
Amigo Imaginario
-Hey Chicos, ¿Queréis conocer a mi nuevo amigo?- Vale!, pero ¿dónde está? - Está justo aquí- ¿Porqué.
Etiquetas :
Curiosidades,
Mathematica 5
Mathematica es un sistema de álgebra computacional originalmente desarrollado por Stephen Wolfram. Mathematica.
Calculo - Tom Apostol
El libro desarrolla el análisis matemático partiendo de las nociones de número hasta llegar a las integrales.
Etiquetas :
Educación Superior,
Libros,
El Submarino
Este entretenido juego es la mejor y más fácil manera de aprender y practicar las cordenadas en el plano.
SERIE DE MATEMÁTICA: Estructuras Algebraicas
En esta oportunidad ponemos a disposición la colección de monografías científicas: Estructuras Algebraicas,.
Etiquetas :
Educación Superior,
Libros,
Universo Matemático
Universo Matemático es una colección de diez documentales de 24 minutos de duración cada uno de índole.
Etiquetas :
Universo Matemático,
Videos,
Fibonacci en Barcelona
Las imagenes de arriba corresponde a Barcelona, concretamente a una zona al lado del Passeig de Joan.
Etiquetas :
Curiosidades,
