Archive for octubre 2009
142857
Al continuar multiplicando por 8, la particularidad antes descrita permanece, pero un poco menos evidente.
Obsérvese que la cifra 7 ha desaparecido, pero ha sido reemplazada por 1 y 6: 1+6=7.
142857 × 9 = 1285713
Chat Noir: juego en flash
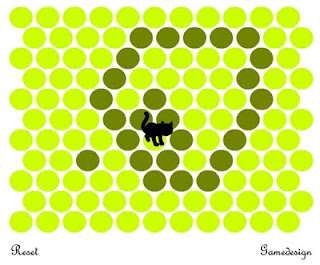
Chat Noir es un juego en flash en el que deberás evitar que el gato escape del tablero. Para ello deberás bloquearle el paso cambiando de color los círculos. Tras unas cuantas partidas podrás comprobar que el dichoso gato es muy difícil de parar, aunque no imposible.
Nunca dividas por cero
En Infinity Squared [Youtube, 4:13 min] se intenta explicar lo que sucede cuando se genera una división por cero, comparándolo con un bug de lo que en el corto se denomina totalityofexistence. La animación es muy vistosa y esta realizada con Legos.
Puzzle con números romanos
IX - XII = III
1, 11, 21, 1211, 111221, 312211, ...
Los problemas de secuencias numéricas son clásicos en las matemáticas recreativas. La secuencia de números enteros "look and say" fue introducida y analizada por el matemático John Conway. Esta secuencia tiene la forma: 1, 11, 21, 1211, 111221, 312211, ... Su construcción es sencilla, cada término describe al anterior:
1 contiene "un uno", o sea, 11; 11 contiene "dos unos", o sea, 21;
21 contiene "un dos y un uno", o sea, 1211;
1211 contiene "un uno, un dos y dos unos", o sea, 111221;
111221 contiene "tres unos, dos doses y un uno", o sea, 312211.
En esta secuencia solo se emplean los números 1, 2, y 3. Otra curiosidad de esta secuencia observada por Conway es que muestra similitud formal con el comportamiento de los elementos químicos. También es curioso que el tamaño de cada secuencia es 1,303577...(constante de Conway) veces mayor que la anterior.
